[python/ML] 회귀 - 경사하강법, 오차역전파

안녕하세요. 오늘은 선형회귀를 푸는 알고리즘 중 하나인 경사하강법, 오차역전파에 관련한 포스팅을 진행하겠습니다.

그 전 포스팅에서 회귀문제를 풀 때는

y = wx + b 

(w는 가중치, b는 절편)

위의 식에서 데이터를 잘 예측할 수 있게 해주는 w,b값을 찾는 과정을 거쳐야 한다고 언급하였습니다.

이번 포스팅은 이 과정이 어떻게 진행되어 최적값을 찾는지 알아보는 시간을 갖도록 하겠습니다.

 

데이터 준비

데이터는 이전 포스팅에도 사용한 공부시간 및 시험점수 데이터를 사용하겠습니다.

https://www.kaggle.com/jahidsizansani/students-study-hour

Students Study Hour

위의 링크에 들어가 csv파일을 다운받아 주세요.

데이터 확인

다음으로 다운받은 csv파일을 판다스로 확인해보도록 하겠습니다.

## 판다스로 데이터 확인 ##
import pandas as pd
study = pd.read_csv('Student Study Hour V2.csv')
print(study.shape)
study.head()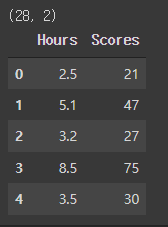

독립변수 및 종속변수 설정

우리는 공부하는 시간에 따른 시험 점수를 예측하고 싶습니다.

이 때, 이 문제를 풀 때 필요한 독립 및 종속변수를 설정해 줍니다.

독립변수(x)는 공부시간(Hours), 종속변수(y)는 시험점수(Scores)로 설정하겠습니다.

## 독립 및 종속변수 설정 ##
x_study = list(study['Hours'])
y_study = list(study['Scores'])

여기서 이제 y = wx + b 라는 식에 가중치(w)와 절편을(b) 찾아야 합니다.

이를 경사하강법을 사용하여 찾아보도록 하겠습니다.

선형회귀- 경사하강법

경사하강법은 기울기(변화율)를 사용하여 모델을 조금씩 조정하여 최적의 모델을 찾는 알고리즘입니다.

경사하강법은 아래와 같은 단계로 진행됩니다.

1. 랜덤으로 w와 b 정하기(랜덤숫자로 모델 만들기)
2. x값 중 하나를 선택해서 y값(예측값 구하기)
3. 2번에서 구한 예측값 y와 2번에서 사용한 x값의 실제 y(결과)값 비교
4. 예측값과 실제값이 거의 같아지도록 w,b 조정(모델 조정)
5. 데이터셋의 모든 x값을 처리할 때까지 2~4번 내용 반복

step1. 가중치(w)와 절편(b) 초기화

랜덤으로 w와 b의 값을 정합니다.

여기서는 1이라는 숫자를 각각 w와 b로 할당하여 모델을 만들어 보도록 하겠습니다.

# 1. w와 b를 초기화(랜덤으로 값 정함)
w = 1
b = 1
##이 떄 랜덤으로 만들어진 모델은 y = x + 1

위에서 만들어진 y = x + 1을 가지고 예측값을 구해 보겠습니다.

 

step2. x값을 대입하여 예측값 구하기

x값으로 위에서 만든 공부시간 리스트 중 0번째 값을 사용하여 예측값 y를 구하는 방법은 아래와 같습니다.

# 2. 랜덤 x값 넣어서 예측값 구해보기
y_model = x_study[0] * w + b
y_model

 3.5

실제 y의 값은

##실제 y값
y_study[0]

21

입니다. 원래의 값과 많은 차이가 있음을 확인할 수 있습니다.

 

step3. 예측값과 실제값의 차이 비교

#3. 예측값과 실제값의 차이 비교
y_study[0]-y_model

17.5

차이가 크네요. 가중치를 더 늘려야 할 것으로 보입니다.

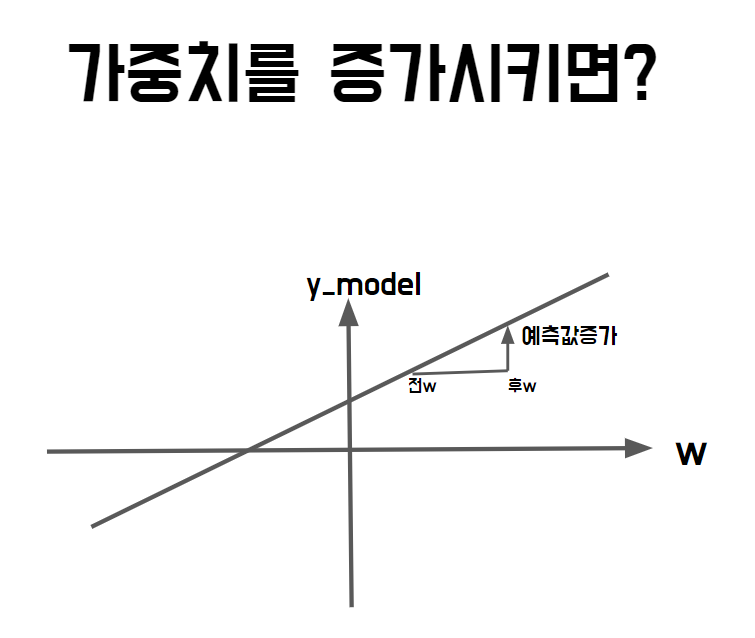
step4. w(가중치)변경하여 예측값 구하기

가중치(w)를 0.1 만 증가시켜 다음 예측값을 측정해 보겠습니다.

#4. w(가중치)를 변경하여 예측값 측정
w_add = w + 0.1
y_model_add = x_study[0] * w_add + b
y_model_add

3.75

그전 결과인 3.5보다 조금 증가함을 확인 가능합니다.

step5. w의 증가량에 대비해 예측값이 얼마나 증가했는지 계산

이 때, 가중치가 전보다 0.1 늘었을 때 y_model이 얼마나 증가하였는지 변화율을 구해보면 아래와 같습니다.

#5. w가 0.1만큼 증가했을 때 y_model이 얼마나 증가했는지 계산
# =(y_model 증가량 / w 증가량)
w_rate = (y_model_add - y_model) / (w_add - w)
w_rate

2.4999999999

약 2.5 의 변화율이 나왔습니다.

이는 x값의 0번째값과 같습니다.

#위에서 구한 변화율은 x[0] 과 같음
x_study[0]

2.5

즉, w변화율은 x값임을 확인할 수 있습니다.

step6. 변화율로 가중치 w 업데이트

위에서 구한 변화율(w_rate)로 다음에 사용할 가중치를 정하도록 하겠습니다.

# 6. 변화율로 가중치 업데이트
w_new = w + w_rate
w_new

3.4999999999

다음에 사용할 w는 3.49999입니다.

이제 절편 b도 w변화율을 구할 때처럼 b 변화율을 구하여 업데이트 해봅시다.

 

step7. 변화율로 절편 b 업데이트

#7.변화율로 절편 업데이트
#b 증가율에 따른 y_model 값 증가값을 계산 후 변화율 계산
b_add = b + 0.1
y_model_add = x_study[0]*w + b_add
y_model_add

3.6

b도 0.1 만 증가시킨 후 y_model의 예측값을 구해보면 3.6 이라는 값이 나옵니다.

여기서 절편이 전보다 0.1 늘었을 때 y_model이 얼마나 증가하였는지 변화율을 보면,

#다음 절편 값 구하는 과정
b_rate = (y_model_add - y_model) / (b_add-b)
b_rate

1.0

1임을 확인할 수 있습니다. 0.1이 아니라 다른 값을 추가하여 변화율을 구하여도 1이 됩니다.

때문에 다음 스텝에서 진행할 새로운 절편 b의 값은 아래와 같습니다.

# 다음 스텝에서 진행할 새로운 b값
b_new = b + 1
b_new

2

경사하강법은 이 방법을 계속 반복하여 최적의 모델을 찾게 됩니다.

하지만, 이는 (1)예측값이 실제 값보다 한참 작은 경우 큰 폭으로 변화율을 줄 수 없고,

(2)예측값이 실제값 보다 큰 상황에서는 변화율을 감소시켜야 하는데 감소시킬 수 없다는 문제점이 있습니다.

이를 해결하기 위한 방법이 바로 '오차역전파(backpropagation)' 입니다.

오차역전파(backpropagation)

오차역전파는 실제값과 예측값의 차이를 이용하여 w와 b를 정합니다.

찾는 방법은 아래와 같습니다.

1. 오차와 변화율을 곱해 다음에 사용할 새로운 가중치 정하기
2. 1번에서 구한 가중치로 다음 x값에 적용하여 업데이트할 가중치 정하기

step1. (변화율 x 오차)로 가중치 업데이트

실제값 - 예측값을 하여 오차를 구하고,

그 오차를 각 w,b의 변화율에 곱한 후 그 값을 더하여 다음에 사용할 새로운 w,b 값을 만듭니다.

#1.변화율 * 오차로 가중치 업데이트
error = y_study[0] - y_model
w_new = w + w_rate *error
b_new = b + 1*error
w_new, b_new

(44.749999999999964, 18.5)

이제 이 각각의 값을 가진 모델을 만들어 공부시간x중 첫번째 값을 넣어 결과를 확인하여 

오차를 구해 가중치를 업데이트해 나갑니다.

#2. x_study[1]을 사용해 오차를 구하고 1번과정과 마찬가지로 그 다음의 w,b값 찾기
y_model = x_study[1] * w_new + b_new
error = y_study[1] - y_model
w_rate = x_study[1] #x값 자체가 변화율이므로
w_new = w_new + w_rate * error
b_new = b_new + 1 * error
w_new, b_new

(-973.8474999999988, -181.2249999999998)

위를 모든 x값을 대입하며 반복하여 최적의 모델을 찾아냅니다.

#모든 x값 반복하여 w,b구하기
for x_i, y_i in zip(x_study,y_study):
  y_model = x_i*w+b
  error = y_i - y_model
  w_rate = x_i
  w = w+w_rate*error
  b = b + 1*error

w, b

(-3.7026494779228295e+34, -5.968245924096763e+33)

위의 값을 이용해 시험점수를 구하면 아래와 같습니다.

y_hat = -3.7*x_study[0] + -5.97
y_hat

-15.219999999999999

아직도 실제 값인 21과는 전혀 다릅니다.

때문에 전체 x값을 20번씩 학습하여 최적의 모델을 찾아보도록 하겠습니다.

학습을 진행하다 inf 값이 나오면 더이상 최적의 값은 없다고 가정후 

학습을 중단하여 w,b 값을 반환하겠습니다.

#학습 반복하여 더욱 향상된 모델 찾기
for i in range(1,20):
  for x_i, y_i in zip(x_study,y_study):
    y_model= x_i*w+b
    if y_model == float('inf'):
      break
    else:
      error = y_i - y_model
      w_rate = x_i
      w = w+w_rate * error
      b = b+1*error
w,b

(7.3379121105182e+307, 2.3866622236073046e+307)

최종 w,b값이 나왔습니다.

이를 모델로 하여 결과를 구해보도록 하겠습니다.

new_ymodel = 7.34*x_study[0] + 2.39
new_ymodel

20.740000000000002

y_study[0]

21

위의 모델이 예측한 값과 실제값이 거의 일치함을 확인할 수 있습니다.

데이터와 가장 잘 맞는 수식 결과

전체 코드

https://colab.research.google.com/drive/1QFzjlztSWllPwjV4pJQRjr3zDVbkdpeH?usp=sharing 

ML동작방법.ipynb

전체코드를 링크로 공유하오니 필요하신 분들은 사본을 만들어 사용하시면 됩니다:)

참고자료

책 - 정직하게 코딩하며 배우는 딥러닝 입문

마무리

저번 시간에 이어 회귀문제에서 어떻게 최적의 모델을 찾아가는지 그 과정을 자세히 알아보았습니다.

관련한 질문이 있거나 다음에 배우고 싶은 내용이 있다면 댓글 남겨주세요 :)

항상 제 글을 읽어주셔서 감사합니다.^0^